| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 논문
- rl
- reinforcement learning
- machine learning
- optimization
- 판다스
- David Silver
- Linear algebra
- ML-Agent
- 리스트
- paper
- 김성훈 교수님
- list
- neural network
- Deep Learning
- pandas
- 딥러닝
- 사이킷런
- 모두를 위한 RL
- 데이터 분석
- Series
- Laplacian
- unity
- Jacobian Matrix
- Hessian Matrix
- 강화학습
- convex optimization
- 유니티
- statistics
- Python Programming
RL Researcher
Playing Atari with Deep Reinforcement Learning 본문
Playing Atari with Deep Reinforcement Learning
Lass_os 2021. 2. 15. 12:161. Abstract
- High-Dimensional Sensory Input으로부터 RL을 통해 Control Policy를 성공적으로 학습하는 DL Model을 선보입니다.
- Paper에서 구현한 Atari Game의 모델은 CNN이며, 변형된 Q-Learning을 사용해 학습되었습니다.
- Paper에서의 Q-Learning이란 input이 raw_pixel이고, output은 미래의 보상을 예측하는 Value function입니다.
- 게임을 학습할 때, 픽셀값들을 입력으로 받고, 각 행동에 대해 점수를 부여하고, 어떤 행동에 대한 결과값을 함수를 통해 받게 됩니다.
- 2600개 가량의 컴퓨터 게임들을 학습시키는데 동일한 모델과 학습 알고리즘을 사용했고, 성공적인 결과를 보여주었습니다.
2. Introduction
딥러닝을 강화학습에 적용하는 과정에서 몇가지 문제점이 발견되었습니다.
- 지금까지 가장 성공적인 딥러닝 프로그램에서는 직접 Label된 많은 양의 Tranning Data를 필요로 합니다. 반면에 RL Algorithm은 자주 Sparse, Noisy and Delayed한 Scalar Reward Signal에서 학습할 수 있어야 합니다. (RL은 Trial and Error를 통해 Action에 대한 결과를 알기 전까지 시간이 필요합니다. 이러한 Delay는 어려움은 만들어냅니다.)
- 대부분의 딥러닝 알고리즘의 Data Sample들이 독립적인 반면, RL에서는 일반적으로 Correlation이 높은 상태의 Sequence끼리 만난다는 것입니다. (현재 State의 Action이 Next State의 Reward에 영향을 주는 등의 상호연관성이 매우 높습니다.)
- RL에서는 Algorithm이 새로운 Behavior를 배울 때마다 Data의 Distribution이 변하게 되는데, 이것은 Data의 Distribution이 고정되어 있다고 가장하는 DL의 Assumption과 충돌하여 문제가 될 수 있습니다.
Paper에서는 CNN이 복잡한 RL환경에서 원시 비디오로부터 성공적인 Control Policy를 학습할 수 있음을 증명합니다. CNN은 변형된 Q-Learning을 통해 학습되며, Network는 weight를 업데이트하기 위해 Stochastic gradient descent를 사용합니다. 또한 Correlated data와 non-stationary distributions의 문제를 약화시키기 위해 Experience Replay Memory를 사용하는데, 이것은 무작위로 이전의 transition을 추출해 Training distribution이 원활해지게 합니다.
DeepMind에서는 하나의 NN을 만들어 가능한 많은 게임을 학습시키는 것을 목표로 하였고, 게임에 대한 특정 정보나 게임의 우위를 위한 데이터들을 전혀 제공하지 않았습니다. 오직 Video의 Visual Data와 Reward 그리고 Terminal으로부터 오는 신호 그리고 가능한 몇개의 Action으로만 학습을 진행하였습니다. 또한 다양한 게임들에 대해 동일한 Network Architecture와 Hyperparameter를 사용하였습니다. (시도한 7개의 게임 중에 6개에서 이전 모든 RL Algorithm을 능가했으며 그 중 3개에서 사람이 직접 플레이한 것을 능가하였습니다.)
3. Background
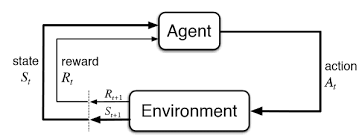
Agent가 Environment와 상호작용하는 작업을 생각해보겠습니다.(이 경우에 Atari emulator는 일련의 작업이나 관찰 보상입니다) 각 time-step마다 Agent는 할 수 있는 Action($a_{T}$)들 중 하나를 선택하게 됩니다. Action이 Emulator로 전달되면 Emulator는 내부 상태와 게임 점수를 수정합니다. 여기서 Agent는 내부 상태를 알 수 없습니다. 단지 화면을 나타내는 Raw pixel의 vector로 이루어진 이미지와 Game score의 변화를 나타내는 Reward($r_{t}$)만을 전달받습니다.
=> 매 time-step마다 Agent가 Action($a_{t}$)를 선택하면 Emulator를 통해서 State를 수정하고 Reward($r_{t}$)가 return됩니다.
하지만 게임의 점수는 현재의 행동뿐만 아니라 이전에 거쳤던 일련의 행동에 의존하여 결정되고, 행동에 대한 피드백은 수천회의 time-step이 진행된 후에 받게 됩니다.
- Agent는 매 time-step마다 할 수 있는 행동들 ($A = {1, ...., K}$)중에서 한가지($a_{t}$)를 선택
- 입력(Image)를 바탕으로 어떤 Action($a_{t}$)을 통해 Reward($r_{t}$)를 받고 다음 State($s^{'}$)를 갱신
- 현재의 Action이 미래에 영향을 받으므로 행동의 Sequence $s_{t} = x_{1}, a_{1}, x_{2},a_{2}, ..., a_{t-1}, x_{t}$를 통해 학습을 진행
- Future에 cumulative Reward를 최대화하는 행동을 선택하도록 학습
하지만 Agent는 오직 현재의 장면만 관찰하기 때문에, 전체적인 상황을 이해하기 힘듭니다. 그래서 이를 해결하기 위해 Action의 Sequence를 관찰하고 이를 통해 학습을 진행합니다. 이러한 Formalism은 크지만 유한한 MDP를 야기하는데, 여기서 각 Sequence는 별개의 State에 해당합니다. 결과적으로 우리는 MDP에 Standard한 RL Method를 적용할 수 있고, 이것은 시간 t에서의 상태를 표현하기 위해 전체 Sequence를 사용함을 의미합니다. Agent의 목표는 Cumulative Reward를 Maximise하는 방식으로 Action을 선택하고 이를 Emulator에 전달하는 것입니다. 시간이 오래 지날수록 Reward의 가치는 점점 내려가는데, 이것은 기호로는 $\gamma$라고 하며 Discount Factor라고 부릅니다.
$time-step$ $t$에서의 Discount Factor가 정의된 Reward를 $R_{t}$라고 할 때, 해당 값은 아래와 같이 정의됩니다.
$$R_{t} = \sum_{t^{'} = t}^{T}\gamma^{t^{'}-t}r_{t^{'}}$$
위의 식에서 T는 Game이 종료되는 time-step이며, 현재 time-step에서 종료 time-step까지 Reward값에 $t^{'}-t$지수승을 한것이 됩니다. 어떠한 State($s$)를 파악한 후에, 취한 Action($a$)을 통해서 얻을 수 있는 max Expected Value를 반환하는 Optimal Action-Value function인 $Q^{*}(s,a)$를 정의하였는데, 해당 함수에 대한 수식은 아래와 같습니다 여기서 $\pi$는 $s_{t}$에서 $a_{t}$를 Mapping하는 policy Function입니다.
$$Q^{*}(s,a) = \underset{x}{max}E[R_{t} \mid s_{t} = s, a_{t} = a, \pi]$$
Optimal Q-Function은 Bellman Expectation Equation이라는 중요한 특성을 따릅니다.
이 방정식은 Sequence $s^{'}$의 다음 time-step에서의 Optimal $Q^{*}(s,a)$값이 모든 Action $a^{'}$에 알려져 있다면, Optimal 전략은 $r + \gamma Q^{*}(s^{'},a^{'})$의 Expected Value를 최대화하는 것입니다. 이를 수식으로 표현해 보겠습니다.
$$Q^{*}(s,a) = EQ^{*}(s,a) = E_{s^{'}\sim \varepsilon}[r + \gamma\underset{a^{'}}{max}Q^{*}(s^{'},a^{'})\mid s,a]$$
많은 강화학습 알고리즘에서는 Q-Function을 추정하기 위하여 Bellman Equation을 Interative하게 Update합니다.Value Iteration은 매 $i$번쨰 iteration마다 아래와 같은 Procedure를 수행하게 됩니다.
$$Q_{i+1}(s,a) = E[r + \gamma Q_{i}(s^{'},a^{'}) \mid s,a]$$
이러한 Value Iteration Algorithm은 MDP에서 $Q_{i} \rightarrow Q^{*} as \ i \rightarrow \infty$라는 것이 알려져 있습니다.
그러나 Action-value function은 각 Sequence마다 독립적으로 Estimate되기 때문에 이러한 방식은 실제로 impractical합니다. 대신 function approximator를 사용하여 Action-value Function을 적절히 approximate 시킵니다.
$$Q(s,a; \theta) \simeq Q^{*}(s,a)$$
일반적으로 Linear Function으로 Approximate하지만, 간혹 Non-linear Function으로 Approximate하는 경우도 있습니다. Neural Network Function Approximator로 weight $\theta$를 사용하는 것을 Q-Network라고 합니다. Q-Network는 each iteration마다 바뀌는 Loss function $L_{i}(\theta_{i})$를 Minimize시킴으로써 학습을 수행합니다.
$$L_{i}(\theta_{i}) = E_{s,a \sim p(\cdot)}[({y_{i}}-Q(s,a;\theta_{i}))^{2}],where, y_{i} = E_{s^{'} \sim \varepsilon}[r +\gamma \underset{a^{'}}{max}Q(s^{'},a^{'};Q_{i-1}) \mid s,a]$$
여기서 $y_{i}$는 iteration $i$의 target value이며 $p(s,a)$는 behaviour distribution으로 sequence $s$에 대해 action $a$의 probability distribution이다.$\theta_{i-1}$는 Loss function $L_{i}(\theta_{i})$를 optimize할 때 fixed되는데, 학습이 진행되기 전에 고정되었던 supervised learning과는 대조된다. 이러한 네트워크의 Gradient는 아래와 같습니다.
$$\triangledown_{\theta_{i}}L_{i}(\theta_{i}) = E_{s,a \sim p(\cdot);s^{'}\sim \varepsilon}[(r+ \gamma \underset{a^{'}}{max}Q(s^{'},a^{'}; \theta_{i-1}) - Q(s,a;\theta_{i}))\triangledown_{\theta_{i}}Q(s,a;\theta_{i})]$$
Deep-Q Learning 알고리즘은 $\varepsilon$과 별도로 작용하는 Model-Free Algorithm입니다. Behaviour Policy와 Learning Policy를 별도로 두는 Off-Policy를 사용합니다. $\epsilon$의 확률로 Random Action을 선택하고 $1-\epsilon$의 확률로는 $a = \underset{a}{max}Q(s,a;\theta)$인 Greedy Strategy를 따릅니다.
일반적으로 RL의 데이터들은 Correlation이 상당히 높습니다. 그러므로 이러한 Data들 사이의 Correlation을 깨기 위해 일정한 확률로 Random action을 선택하고, 남은 확률로는 greedy strategy를 따라 행동을 선택합니다.
4. Related Work
이전에 RL이 적용되었던 가장 유명한 사례는 TD-gammon입니다. 강화학습을 통해 스스로 플레이 방법을 터득하고, Q-Learning과 유사하게 Model-Free구조로 Multi-Layer Perceptron with One Hidden Layer의 Network를 가졌습니다.
하지만 TD-gammon의 방식을 GO나 Chess에 적용을 할 때면 실패하였고, 이러한 접근법은 TD-Gammon에만 최적화되었으며 어쩌면 주사위의 확률이 우연하게 탐험을 돕고, Value funtion을 smooth하게 만들어 주었다는 착각을 불러일으켰습니다.
또한 Q-Learning과 같은 Model-Free Reinforcement Learning 알고리즘을 Non-Linear Function Approximator나 Off-Policy Learning에 적용시키면 Q-network가 발산하며, 수렴을 위해 주로 Linear Function Approximators에 초점을 두고 RL이 진행되도록 초래하였습니다.
그리고 최근에야 DL과 RL을 융합시키는 분야가 부활하게 되었습니다. Deep Neural Network는 Environment를 측정하기 위해 사용되게 되었고, Restricted Boltzmann 기계들은 value function이나 policy를 측정하기 위해 사용되기 시작하였다. 게다가 발산문제는 gradient temporal-difference에 의해 다루어지게 되었고, 이것은 non-linear function approximator로 fixed policy를 사용할 때나 제한적인 Q-Learning의 변형을 활용하여 linear function approximation과 함께 control policy를 학습할 때 수렴함을 증명하였습니다. 그러나 이것은 nonlinear control 까지 확정되지는 않은 상태였습니다.
우리의 접근법과 가장 유사했던 이전의 작업으로는 Neural fitted Q-Learning(NFQ)가 있다. NFQ는 Q-Network의 Parameter들을 갱신시키기 위해 RPROP 알고리즘을 사용하여 2번 방정식에서의 Loss Function을 최적화시켰다. 그러나 이것은 Iteration을 돌기 위해 많은 계산 양을 필요로하는 Batch Gradient Descent를 사용하였지만, 이 논문에서는 Stochastic Gradient Descent를 사용하여 Iteration을 돌기 위해 필요한 계산 양을 줄였고, 큰 Data-Set까지 학습을 Scale-up 시켰다. NFQ는 또한 처음으로 deep autoencoder를 사용함으로써 task의 low dimensional representation을 학습하였고, 시각입력을 사용함으로써 real-world control task를 성공적으로 NFQ 알고리즘에 적용하였다. 그러나 이와 반대로 우리는 시각적 입력으로부터 직접적으로 철저한 강화학습을 적용시켰고, 결과적으로 Action-Value를 판별하는 것과 같은 특징들을 학습하였다.
RL 플랫폼으로 사용된 Atari 2600 에뮬레이터는 visual features와 linear function approximation을 standard RL에 적용시켰던 [3] 논문에서부터 사용되기 시작하였습니다. 결과적으로 많은 수의 특징들을 lower-dimensional space에 적용시킴으로 결과는 개선되었다. HyperNEAT evolutionary architecture는 Atari Platform에도 적용되었으며, 이 플랫폼은 각 게임마다 전략을 나타내는 Neural Network를 발전시키는데 사용되었습니다. Emulator의 리셋 기능을 사용하여 결정을 내리는 Sequence에 대해 반족적으로 교육을 받았을 때, 이러한 전략은 여러 아타리 게임에서의 디자인 결함을 악용할 수 있었습니다.
5. Deep Reinforcement Learning
Computer Vision과 Speech Recognition에서 이뤄낸 최근의 성과는 매우 큰 training sets를 활용하여 deep neural network를 효과적으로 훈련시킨 결과였습니다. 대부분의 성공적인 approaches는 Stochastic Gradient Descent를 기반으로 lightweight update함으로써, raw input들로부터 직접 학습된 것입니다. Deep Neural Network에 충분한 양의 Data를 제공함으로써, handcrafted된 features보다 많은 representation들을 학습할 수 있었고, 이러한 성공들을 바탕으로 RL에 대한 우리의 접근법을 생각해냈습니다. 우리의 목표는 RL 알고리즘을 Deep Neural Network와 연결하여 RGB Image들에 직접적으로 작동하고, Stochastic Gradient Updates를 사용하여 Traning Data를 효율적으로 처리하는 것입니다.
TD-Gammon과 달리 우리는 experience replay라는 기술을 활용하였는데, Agent가 매 Time-Step마다 했던 Experience(Episode)들을 Dataset에 저장을 시키고, 수많은 Episode들이 replay memory에 쌓이게 된다. 그리고 알고리즘 내부에서 샘플들이 저장된 풀로부터 임의로 하나를 샘플링하여 학습(Q-Learning, Mini-Batch)에 적용시켰다습니다. 이후에(experience replay 후) Agent는 e-greedy policy에 따라 행동을 선택하고 수행합니다. Neural Network의 입력으로써 가변적인 history를 사용하는 것은 어렵지만, Deep-Q Algorithm에서는 ϕϕ 함수를 사용하여 고정 길이의 history를 입력으로 사용합니다.
'Reinfrocement Learning > Paper Review' 카테고리의 다른 글
| Human-level control through deep reinforcement learning (0) | 2021.02.15 |
|---|
