| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 모두를 위한 RL
- pandas
- Deep Learning
- machine learning
- 딥러닝
- Series
- unity
- Jacobian Matrix
- neural network
- David Silver
- ML-Agent
- Python Programming
- list
- 김성훈 교수님
- 강화학습
- 논문
- reinforcement learning
- 판다스
- 데이터 분석
- optimization
- 리스트
- Linear algebra
- 사이킷런
- statistics
- 유니티
- paper
- rl
- Laplacian
- convex optimization
- Hessian Matrix
RL Researcher
Lecture 2 : Convex Optimization (Stanford) 본문
Convex sets
- affine and convex sets
- some important examples
- operations that preserve convexity
- generalized inequalities
- separating and supporting hyperplanes
- dual cones and generalized inequalities
Affine set
아래에 그림의 $x_{1}$과 $x_{2}$를 통하는 모든 점들을 Affine set이라고 부름.
$$x = \theta x_{1}+(1-\theta)x_{2}\ \ \ \ \ (\theta \in R)$$
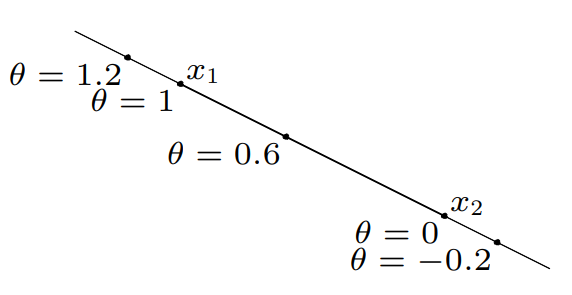
affine set : set에서 두 개의 다른 점을 통과하는 선을 포함함.
example : linear equations $\left \{ x \mid Ax = b \right \}$의 solution set
(반대로 모든 affine set은 선형 방정식의 solution set으로 표현할 수 있음.)
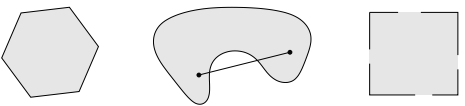
Convex set
line segment(선분) : $x_{1}$과 $x_{2}$ 벡터 사이의 모든 점.
$$x = \theta x_{1}+(1-\theta) x_{2}$$
with $0 \leq \theta \leq 1$
convex set : 두점이 포함되어 있는 선분을 포함하고 있는 것.
$$x_{1},x_{2} \in C, \ \ 0 \leq \theta \leq 1 \Rightarrow \theta x_{1}+(1-\theta) x_{2} \in C$$
example (one convex, two nonconvex sets)
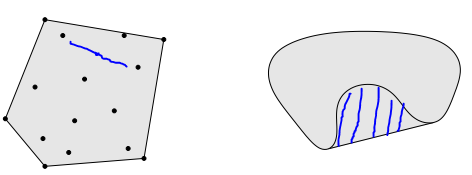
Convex combination and convex hull
convex combination은 line segment의 idea를 Generalized함.
convex combination of $x_{1}, ..., x_{k}$ : form의 모든 점 $x$의 linear combination
$$x = \theta_{1} x_{1} + \theta_{2} x_{2} + \cdots + \theta_{k} x_{k}$$
with $\theta_{1} + \cdots + \theta_{k} = 1, \theta_{i} \geq 0$
convex hull conv S : S의 모든 볼록한 점들의 조합의 set
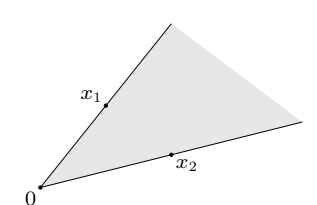
Cone
Cone은 반드시 원점을 포함해야 함. 따라서, 원점에서 시작해서 집합에 속한 점 $x \in C$를 지나는 ray를 만들었을 때 $\theta x \in C$가 되면 집합 $C$를 cone 또는 nonnegative homogenous라고 함.
$\theta x \in C$ with $x \in C, \theta \geq 0$
[참고] Affine set이나 Convex set과는 달리, cone을 정의할 때는 ray의 출발점을 원점으로 가정하고 있기 때문에 집합에 속하는 하나의 점만을 사용해서 정의함.
Convex cone
set $C$가 cone이면서 convex이면 이를 convex cone이라고 하며 다음과 같이 정의됨.
$\theta_{1} x_{1} + \theta_{2} x_{2} \in C$ with $x_{1},x_{2} \in C, \theta_{1},\theta_{2} \geq 0$
아래의 그림에서는 파이 모양의 convex cone을 보여주고 있음. 그림에서는 $x_{1}$과 $x_{2}$는 boundary에 속하는 점으로 $\theta_{1}$과 $\theta_{2}$가 모두 0인 경우 꼭지점이 되고, 둘 중 하나가 0이면 경계선이 되며, 둘 다 0보다 크면 내부의 점이 됨.
Hyperplanes and halfspaces
hyperplane(초평면) : $\left \{ x \mid a^{T}x = b \right \} \ (a \neq 0)$ form을 가진 set
linear equation으로 만들어질 수 있는 특정 평면. 1차일 경우 선, 2차일 경우 평면 등이 됨.
b가 0인 경우에는 원점을 지나감.
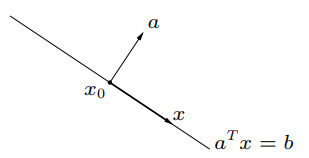
halfspace :
'Optimization > Stanford Lecture' 카테고리의 다른 글
| Lecture 1-Convex Optimization (Stanford) Question (0) | 2021.03.12 |
|---|---|
| Lecture 1 : Convex Optimization (Stanford) (0) | 2021.02.25 |
