Lecture 3: Planning by Dynamic Programming

What is Dynamic Programming?

• 동적 계획법은 큰 문제를 작은문제들로 나누고 작은 문제들의 해결책들을 찾은 후 모아 큰 문제를 푸는 것입니다.

Requirements for Dynamic Programming

• 동적 계획법의 두가지 조건에 대해서 보겠습니다.
  • 큰 문제가 작은 문제들로 나뉠 수 있어야 합니다.
  • Subproblem을 풀면 문제에 대한 정답을 저장해 두었다가 나중에 재사용합니다.
  • MDP는 위 두 조건을 만족합니다.

Planning by Dynamic Programming

• 동적 계획법은 MDP의 모든 지식을 알고 있습니다.
• 동적 계획법이 MDP의 계획에 사용됩니다.
• 쉽게 생각하면, Prediction은 value function을 찾는 문제이고, Control문제는 policy를 찾는 문제입니다.
• Prediction의 경우
  • 입력: MDP $<S,A,P,R,\gamma>$ 그리고 정책 $\pi$
  • 또는: MRP $<S,P^{\pi},R^{\pi},\gamma>$
  • 출력 : 가치함수 $v_{\pi}$
• Control의 경우
  • 입력: MDP $<S,A,P,R,\gamma>$
  • 출력: 최적의 가치함수 $v_{*}$
  • 그리고: 최적의 정책 $\pi_{*}$

Other Applications of Dynamic Programming

• 동적 계획법은 다양한 분야에서 사용됩니다.

Interative Policy Evaluation

• 정책 $\pi$를 따라갔을 때 받을 Return 값이 Evaluation이기 때문에 이것은 Value Function을 찾는 문제라고 볼 수 있습니다.(Prediction문제)
• $v_{1} \rightarrow v_{2} \rightarrow ... \rightarrow v_{\pi}$
• 동기적 백업을 이용합니다.
  • 각 반복은 $k + 1$
  • 모든 스테이트 $s \in S$
  • $v_{k+1}(s) 에서부터 v_{k}(s^{'})$까지 업데이트를 수행합니다.
  • $s$는 다음 $s'$에 있다.

Interative Policy Evaluation (2)

• Bellman Expectation Equation을 이용해서 제일 위의 값을 계속 업데이트 해 나갑니다.

  Evaluating a Random Policy in the Small Gridworld

위의 예제는 정책 평가에 대한 예시입니다.

Iterative Policy Evaluation in Small Grid world

Iterative Policy Evaluation in Small Gridwold (2)

How to Imporve a Policy

• 정책 $\pi$가 주어졌을 때
  • Bellman Expection Equation을 이용한 수식을 통해 정책 $\pi$를 평가합니다.

$$v_{\pi}(s) = E[R_{t+1} + \gamma R_{t+2} + ... \mid S_{t} = s]$$

• greedy하게 행동해서 정책을 개선시킵니다.

$$\pi^{'} = greddy(v_{\pi})$$

Policy Iteraion

Jack's Car Rental

Policy Iteration in Jack's Car Rental

Policy Improvement

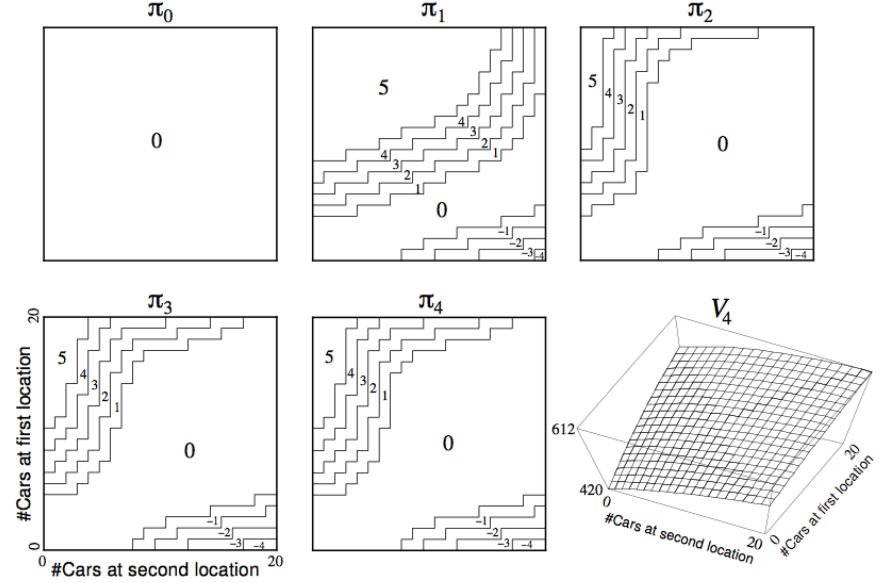
• 결정론적 정책, $a = \pi(s)$
• 저희는 정책을 개선하기 위해서 greedy하게 행동할 수 있습니다.

Policy Improvement (2)

• 제일 처음 수식으로 가게 된다면 향상은 멈추게 됩니다.
• 그 아래의 수식은 Bellman optimality equation은 그 아래의 식을 만족하게 됩니다.
• 결국 $\pi$는 최적의 정책값입니다.

Modified Policy Iteration

• 정책 평가에서 꼭 $v_{\pi}$에 수렴해야 하는가?
• 아니면 조금더 일찍 끝내면 안되는가?
• Grid world예제의 $k=3$이라고 하면 3번 평가하고, 향상하면 안되는 것인가?
• 위의 글은 정책 반복에 대해 충족하게 되는 조건입니다.

Generalised Policy Iteration

Principle of Optimality

• 최적은 두가지 요소로 나누어질 수 있습니다.
  • 첫번째 행동 $A_{*}$은 최적이다.
  • 다음 State $S^{'}$는 최적의 정책을 따라갑니다.

Deterministic Value Iteration

• 작은 문제들의 $v_{*}(s^{'})$을 알게 된다면은 한스텝의 lookahead를 통해서 $v_{*}(s)$ 구할 수 있습니다.
• Bellman optimality Equation을 통해 계산이 가능합니다.(max 때문에 역행렬을 계산할 수 없기 때문에 iteration하게 풀어야 합니다.)

Example: Shortest Path

• 다음의 그림은 최단 거리를 찾는 문제입니다.(Bellman Optimality Equation 사용)

Value Iteration

• 문제 : 최적의 정책 $\pi$를 찾는 것
• 해결책 : 반복적으로 Bellman Optimality Backup을 적용하는 것입니다.
• 정책 반복과는 다르게 가치 반복은 정책이 없습니다.
• 동기적 백업을 사용합니다.
  • 각 반복은 $k + 1$
  • 모든 스테이트 $s \in S$
  • $v_{k+1}(s) 에서부터 v_{k}(s^{'})$까지 업데이트를 수행합니다.
  • $s$는 다음 $s'$에 있다.
• 정책 반복과 달리, 가치 반복에는 명시적인 정책이 존재하지 않습니다.

Value Iteration (2)

Synchronous Dynamic Programming Algorithms

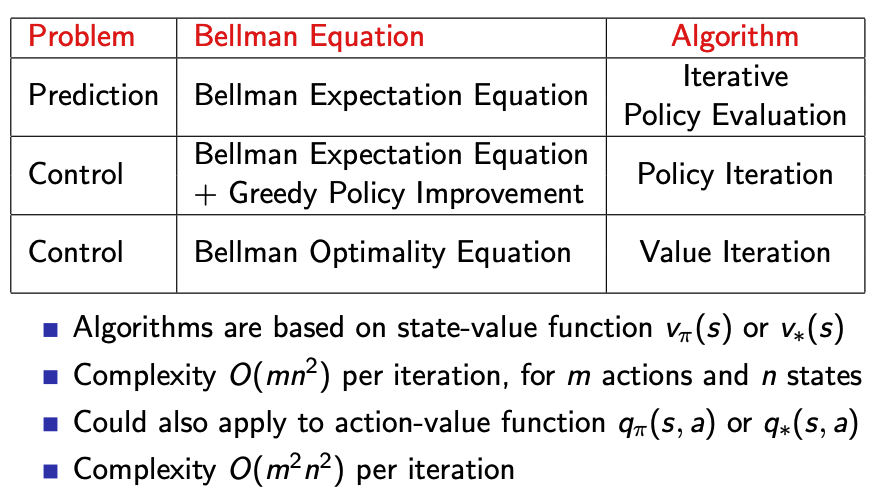
• 동기적 동적 계획 알고리즘은 상태가치 함수 $v_{\pi}(s)$ 또는 $v_{*}(s)$를 기반으로 합니다.
• n개의 State, m개의 행동에 대한 반복당 복잡성은 $O(mn^{2})$입니다.
• $q_{\pi}(s,a)$ 또는 $q_{*}(s,a)$에도 행동 가치함수를 적용할 수 있습니다.
• 반복당 복잡성은 $O(mn^{2})$입니다.

Asynchronous Dynamic Programming

• DP 방법론은 모두 동기적 백업을 이용합니다.
• 모든 State들이 parallel하게 백업이 됩니다.
• Agent가 선택한 각 상태에 대해 적절한 백업을 적용합니다.
• 동기적 백업을 사용할 경우에 계산을 크게 줄일 수 있습니다.
• 모든 상태가 계속해서 선택되게 되는 경우에는 값이 수렴하게 됩니다.

Asynchronous Dynamic Programming

• 위는 비동기적 동적 계획에 대한 세가지 간단한 아이디어에 대해 설명하고 있습니다.

In-Place Dynamic Programming

Prioritised Sweeping

• Bellman 오류의 크기를 이용하여 State에 대한 선택을 안내해 줍니다.

Real-Time Dynamic Programming

• 위의 3가지 그림은 동기적 DP의 예시에 대해서 설명하고 있습니다.

Full-Width Backups

• DP는 Full-Width Backup을 사용합니다.
• 중간 크기의 문제에 대해서만 적용이 가능합니다.(커지면 기하급수적으로 증가)

Sample Backups

Approximate Dynamic Programming

Some Technical Question

Value Function Space

Value Function $\infty$-Norm

Bellman Expectation Backup is a Contraction

Convergence of Iter. Policy Evaluation and Policy Iteration

Bellman Optimality Backup is a Contraction

Convergence of Value Iteration