Lecture 02 : Markov Decision Processes

Inroduction to MDPs

• MDP는 강화학습에서의 환경을 나타냅니다.
• Environment가 모두 관찰가능한 상황일 경우에 이것을 MDP라고 부릅니다.
• 현재의 State가 Process에 대해 완전히 표현하는 것입니다.
• 거의 모든 강화학습 문제는 MDP문제로 정의할 수 있습니다.

Markov Property

• 현재가 있다면 미래는 과거와 독립적이다.

$$P[S_{t+1} \mid S_{t}\ = P[S_{t+1} \mid S_{1}, ..., S_{t}]$$

State Transition Matrix

• Markov State인 $s$ 그리고 다음상태가 $s^{'}$, 상태천이 확률은 다음과 같이 정의됩니다.

$$P_{ss'} = P[S_{t+1} = s' \mid S_{t} = s]$$

• 상태천이 행렬 $P$는 State $s$에서 다음 상태인 $s'$으로 갈때의 천이 확률을 정의합니다.

Markov Process

• Markov Process (또는 마르코프 체인) 은 $<S,P>$로 이루어져 있습니다.
  • $S$는 유한한 State들의 집합입니다.
  • $P$는 상태 천이 확률을 나타냅니다.  

$$P_{ss'} = P[S_{t+1} = s' \mid S_{t} = s]$$

Example : Student Markov Chain

 

Example : Student Markov Chain Episodes

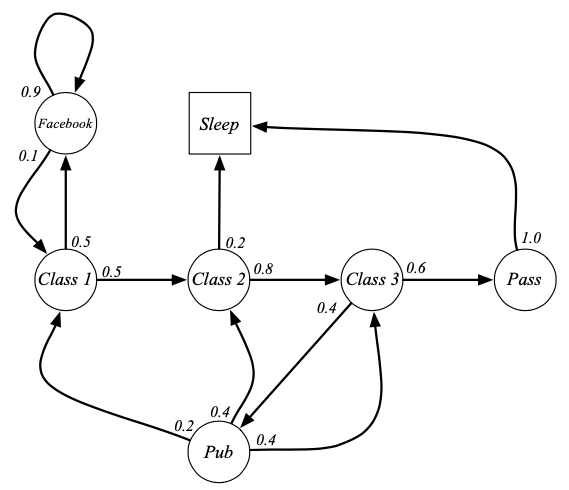
Episode란 시작점부터 Terminal State까지 가는것이 1번의 Episode입니다.

 

 

Example : Student Markov Chain Transition Matrix

Markov Reward Process

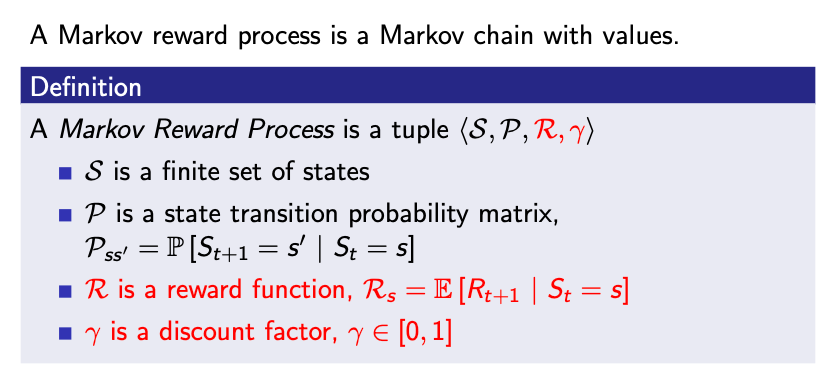
• MRP는 $<S,P,R,\gamma>$값의 튜플로 표현할 수 있습니다.
• $R$은 보상함수이고, $R_{s} = E[R_{t+1} \mid S_{t} = s]$ 로 정의됩니다.
• $\gamma$는 감가율이며, $\gamma \in [0,1]$로 정의됩니다($\gamma$값은 0과 1사이의 실수입니다.) 

Example : Student MRP

Return

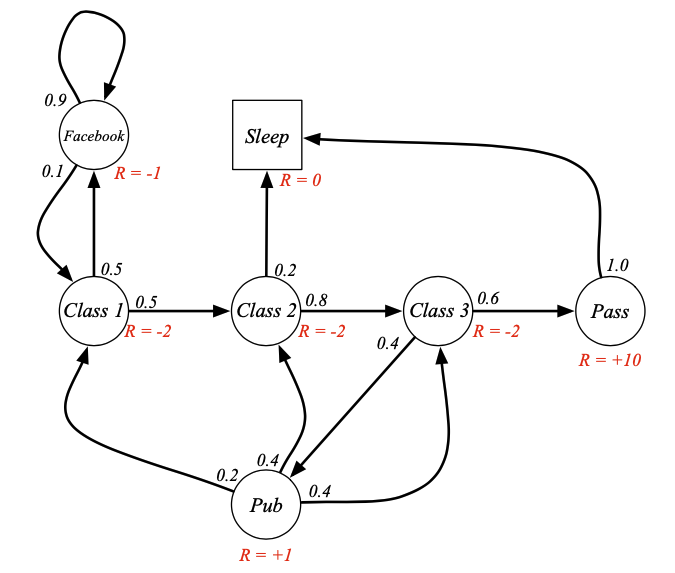
• 강화학습은 Return을 최대화하는 것입니다.
• Return은 $G_{t}$로 표시합니다.
• Return은 미래의 보상을 총 합을 말하지만 미래의 보상에다 감가율을 곱합니다.

$$G_{t} = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}$$

• $\gamma$가 0에 가까워 질수록 "근시" 평가를 하게 됩니다. (즉, 가까운 보상에 대한 것만 평가함)
• $\gamma$가 1에 가까워 질수록 "원시" 평가를 하게 됩니다. (즉, 멀리 있는 보상에 대해 평가함)

Why discount?

• 솔직히 얘기하자면 감가율을 곱하는 이유는 수학적으로 편리하기 때문입니다.
• 이론적인 이야기를 하자면 사람들은 눈앞에 있는 보상을 원하지, 현재와 같은 보상을 미래에 받기를 원하지 않습니다. 예를 들면 지금 만원을 받을것인가, 10년뒤에 만원을 받을 것인가 물어본다면 어떻게 대답할 것인가?
• 어떤 행동을 해도 Terminal State로 갈 때는 $\gamma$를 1로 설정해도 되는 경우가 있습니다.

Value Function

• Value Function은 Return의 기댓값(Expectation Value)입니다.

$$ v(s) = E[G_{t} \mid S_{t} = s] $$

Example : Student MRP Returns

Example : State-Value Function for Student MRP (1)

 

Example : State-Value Function for Student MRP (2)

Example : State-Value Function for Student MRP (3)

Bellman Equation for MRPs

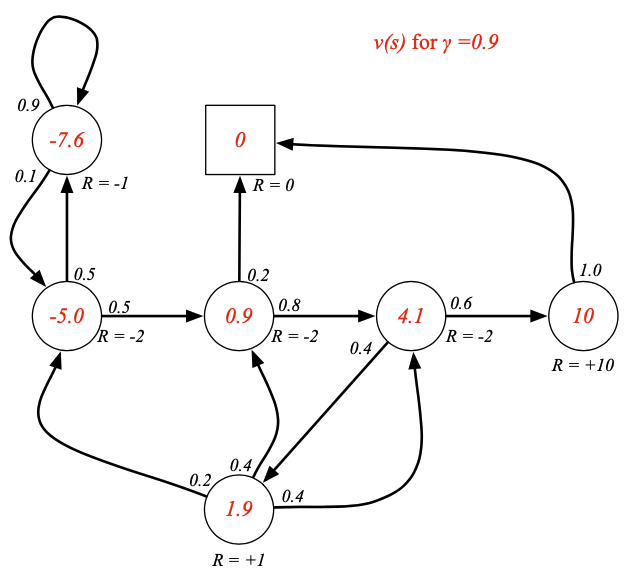
다음 식은 중요한 이론에만 대해서 정의하겠습니다.

• 가치함수는 두개의 부분으로 분해할 수 있습니다.
  • 즉각적인 보상 $R_{t+1}$
  • 다음 State에 대한 할인된 값인 $\gamma v(S_{t+1})$
    • 현재 State에 대한 Value Function은 현재 State에 대한 Return값의 기댓값입니다.
    • 아래의 식은 Return값을 풀어서 쓴 식입니다.
    • 그 뒤 $\gamma$로 묶어줍니다,
    • 묶어서 쓴식은 또 $\gamma$Return값으로 표현할 수 있습니다.
    • 마지막으로 Reutrn값은 다음 State에 대한 Value Function에 Discount Factor를 곱한값으로 표현이 가능합니다.

Bellman Equation for MRPs

 

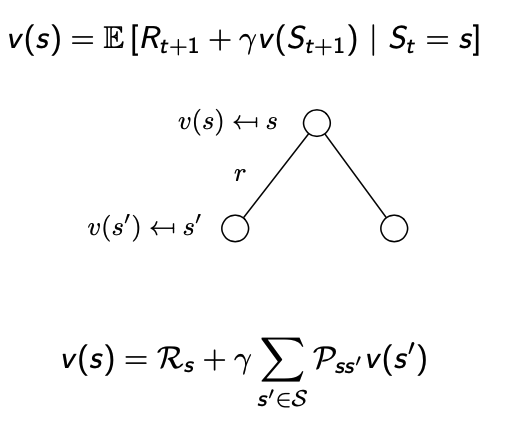
위의 그림은 Bellman Equation의 MRP에 대한 수식을 그림으로 나타낸 것입니다.

Example : Bellman Equation for Student MRP

Bellman Equation for MRPs (2)

• 벨만 방정식은 간결하게 행렬을 사용하여 표현할 수 있습니다.

$$v = R + \gamma Pv$$

Solving the Bellman Equation

위의 수식을 알면 Value function을 한번에 알 수 있습니다.

• 바로 풀 수 있는 방정식은 작은 MRP문제입니다.
• 큰 MRP문제에 대해서 알아보겠습니다.
  • Dynamic-Programming
  • Monte-Carlo evaluation
  • Temporal-Difference learning

Markov Decision Process

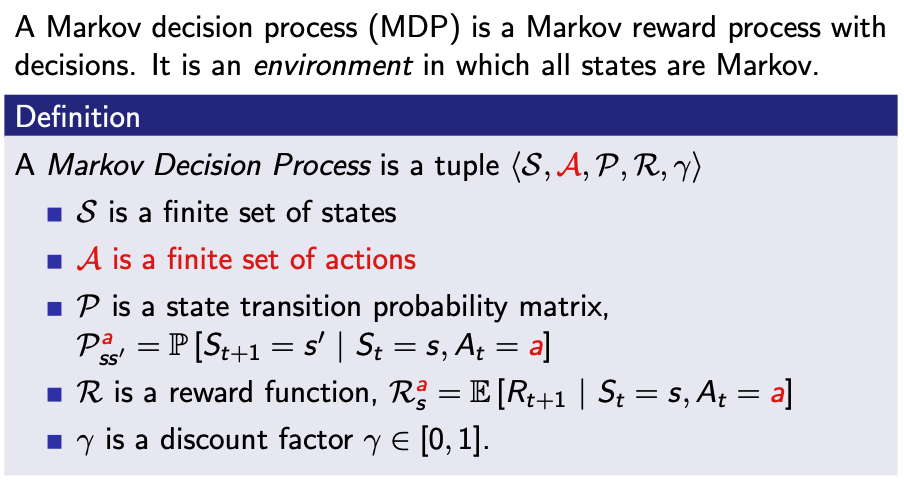
• 간결하게 말하자면 MDP는 MRP에서 Action만 더해진 것입니다.
• MDP는 $<S, A, P, R, \gamma>$로 나타낼 수 있다.
• $A$는 행동에 대한 유한한 집합입니다.
• 이때 $P$는 상태천이 행렬입니다.

$$P_{ss'}^{a} = P[S_{t+1} \mid S_{t} = s,A_{t} = a]$$

Example : Student MDP

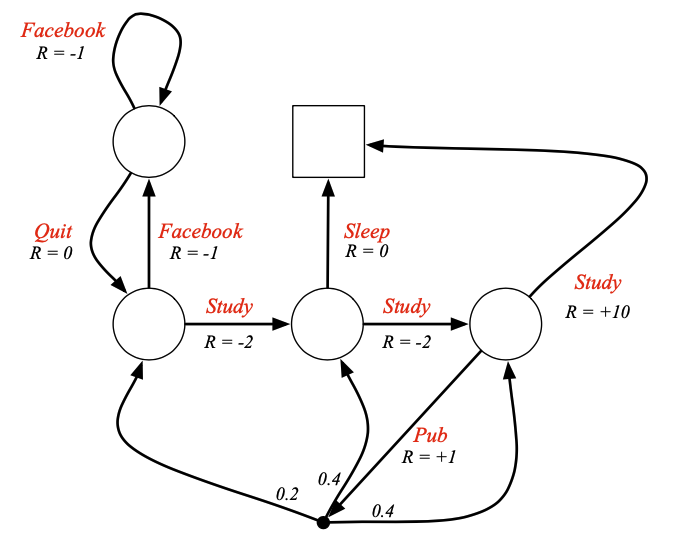
MRP에서는 State마다 Reward가 주어졌지만 MDP는 Action마다 Reward가 주어집니다.  

 

Policies (1)

• 정책 $\pi$는 State가 주어졌을 때의 action 분포값입니다.

$$\pi(a \mid s) = P[A_{t}=a \mid S_{t} = s]$$

• policy는 Agent의 행동을 완전히 결정해줍니다.
• MDP에서의 Policy는 현재 State만 있다면 구할 수 있습니다.

Polices (2)

• MDP $M = <S,A,P,R,\gamma>$ 그리고 정책 $\pi$
• 수열 State $S_{1},S_{2},...$는 Markov Process $<S, P^{t}>$
• 보상의 수열 $S_{1},R_{2},S_{2},...$는 MRP $<S,P^{\pi},R^{\pi},\gamma>$

$$P_{s,s'}^{\pi} = \sum_{a \in A}\pi(a \mid s)P_{ss'}^{a}$$

$$P_{s}^{\pi} = \sum_{a \in A}\pi(a \mid s)R_{s}^{a}$$

Value Function

• 어떤 State에 대한 가치함수 $v_{\pi}(s)$는 policy $\pi$를 따라갑니다.(상태가치함수)

$$v_{\pi}(s) = E_{\pi}[G_{t} \mid S_{t} = s]$$

• 어떤 State에 대한 행동가치함수  $q_{\pi}(s,a)$는 정책 $\pi$를 따릅니다.(행동가치함수)

$$q_{\pi}(s,a) = E_{\pi}[G_{t} \mid S_{t} = s, A_{t} = a]$$

Example : State-Value Function for Student MDP

Bellman Expectation Equation

벨만 기댓값 방정식

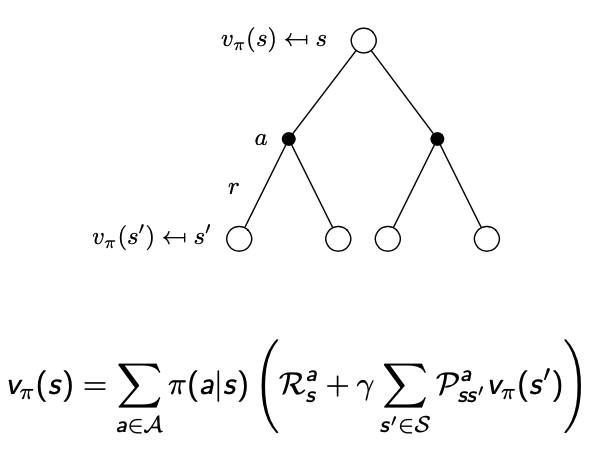
• 상태가치함수에 대해 표현하겠습니다.

$$v_{\pi}(s) = E_{\pi}[R_{t+1} +\gamma v_{\pi}(S_{t+1}) \mid S_{t} = s]$$

• 행동가치함수에 대해 표현하겠습니다.

$$q_{\pi}(s,a) = E_{\pi}[R_{t+1} + \gamma q_{\pi}(S_{t+1}, A_{t+1})\mid S_{t} = s, A_{t} = t]$$

 

Bellman Expectation Equation for $V^{\pi}$

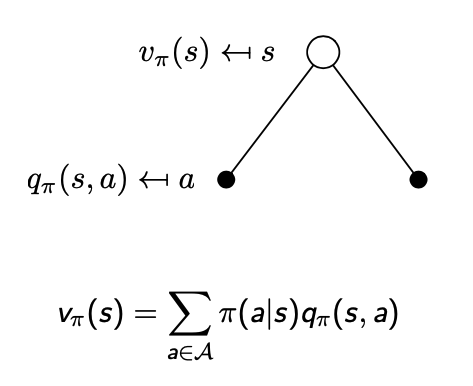
• 위의 그림은 상태가치함수에 대한 수식표현입니다.

Bellman Expectation Equation for $Q^{\pi}$

• 위의 그림은 행동가치함수에 대한 수식표현입니다.

Bellman Expectation Equation for $v_{\pi}$ (2)

Bellman Expectation Equation for $q_{\pi}$

Example : Bellman Expectation Equation in Student MDP

Bellman Expectation Equation (Matrix Form)

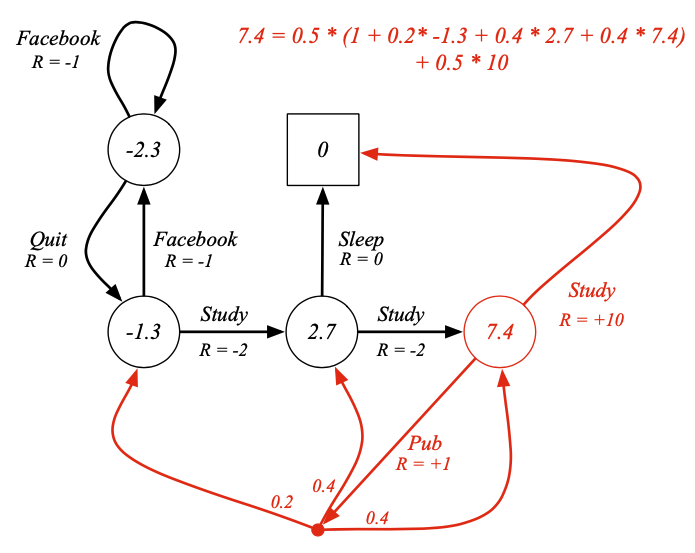
위의 그림은 벨만 기댓값 방정식을 행렬적으로 나타낸 것입니다.

Optimal Value Function

최적가치함수에 대해서 알아보겠습니다.

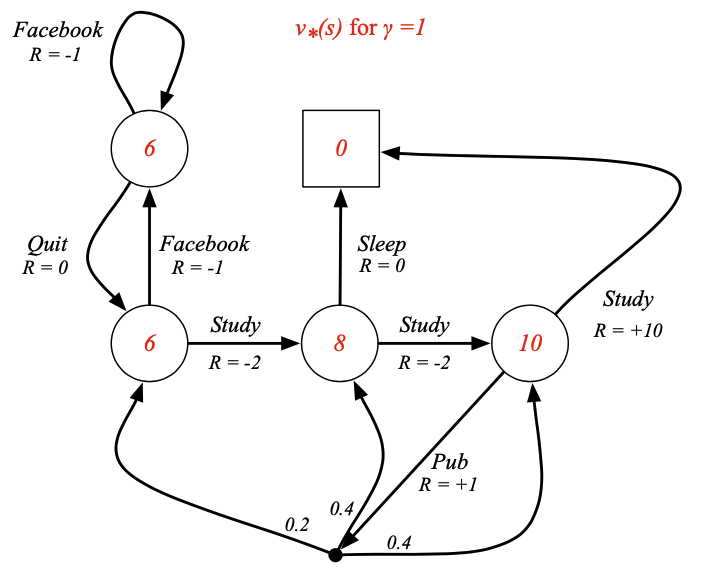
• 최적의 상태가치함수 $v_{*}(s)$는 모든 정책값을 최대화한 값입니다.

$$v_{*}(s) = \max_{\pi} v_{\pi}(s)$$

• 최적의 행동가치함수 $q_{*}(s,a)$는 행동값을 최대화하는 정책을 따른 것입니다.

$$q_{*}(s,a) = \max_{\pi}q_{\pi}(s,a)$$

※ MDP를 풀었다는 것은 우리는 최적의 가치함수를 찾았다는 말과 동일하다고 정의할 수 있습니다.

Example : Optimal Value Function for Student MDP

Example : Optimal Action-Value Function for Student MDP

Optimal Policy

Finding an Optimal Policy

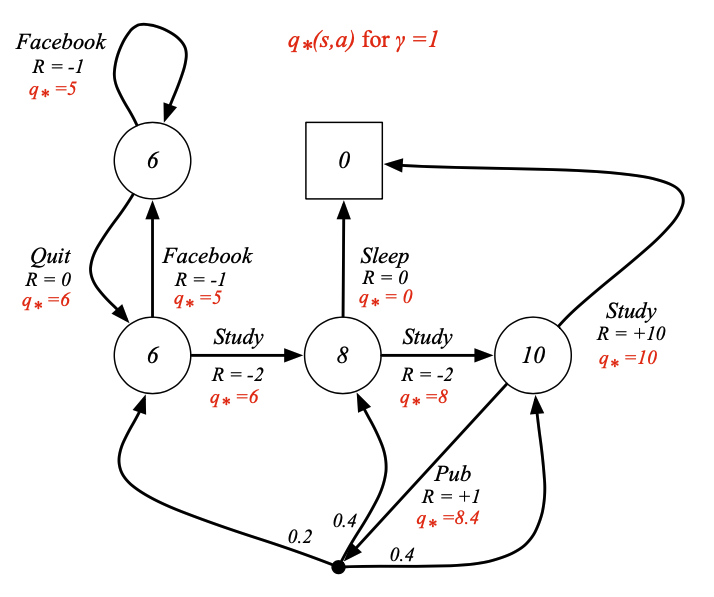
• 최적의 정책은 행동가치를 최대화하는 것을 찾았을 때의 가정입니다.
• 위의 수식은 최대화하는 행동가치함수의 action을 찾았을 때 어떤 MDP이던 결정론적 최적 정책이 존재합니다.(왜냐? 최댓값은 1, 나머지는 0이기 때문 본질은 Policy는 Stochastic이지만 위의 수식은 Deterministic이다.)
• 우리는 행동가치함수 $q_{*}(s,a)$를 찾았다고 할 때 즉각적으로 최적의 정책을 가지고 있다고 볼 수 있습니다.

Example: Optimal Policy for Student MDP

Bellman Optimality Equation for $v_{*}$

Bellman Optimality Euation for $Q^{*}$

Bellman Optimality Equation For $V^{*}$ (2)

Bellman Optimality Equation For $Q^{*}$ (2)

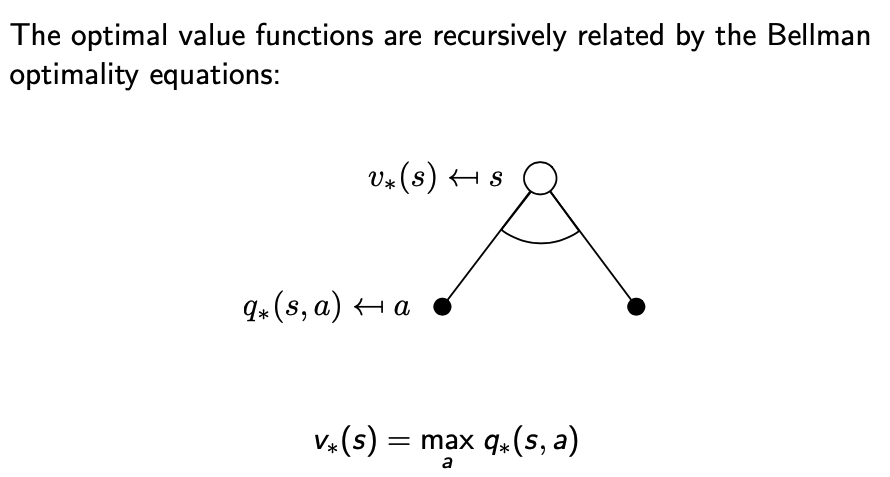
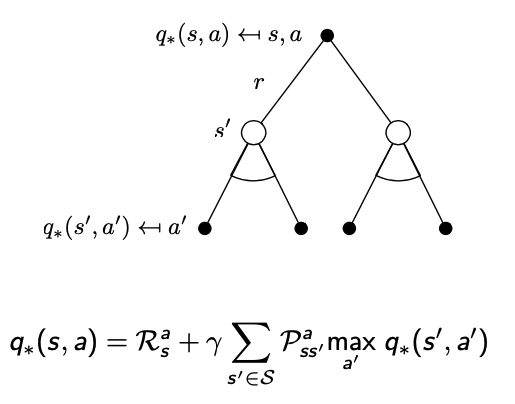
max가 있기 때문에 Linear하지 않습니다(결론적으로 수식을 풀어서 사용할 수 없습니다.)

Example : Bellman Optimality Equation in Student MDP

Solving the Bellman Optimality Equation

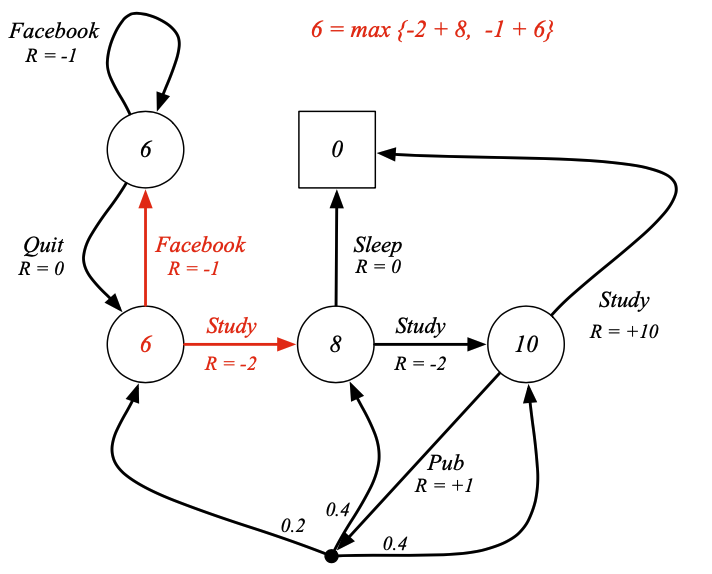
• 벨만 최적 방정식은 선형적이지 않습니다.
• 해가 존재하지 않습니다.
• 많은 반복적인 해결책들이 존재합니다.
  • 가치반복
  • 정책반복
  • Q-Learning
  • 살사