Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 유니티
- Linear algebra
- 김성훈 교수님
- Laplacian
- neural network
- 데이터 분석
- pandas
- David Silver
- optimization
- Hessian Matrix
- Deep Learning
- 논문
- statistics
- unity
- 사이킷런
- 판다스
- rl
- convex optimization
- Series
- Jacobian Matrix
- reinforcement learning
- 딥러닝
- ML-Agent
- 강화학습
- 리스트
- 모두를 위한 RL
- machine learning
- paper
- list
- Python Programming
Archives
RL Researcher
Line Segment 본문
우선 $\mathbb{R}^{n}$ 차원에 대해서 정의하면, $\mathbb{R}^{n}$ 차원 공간의 elements는 n-component vector $x=[x_{1},x_{2},...,x_{n}]^{T}$이다.
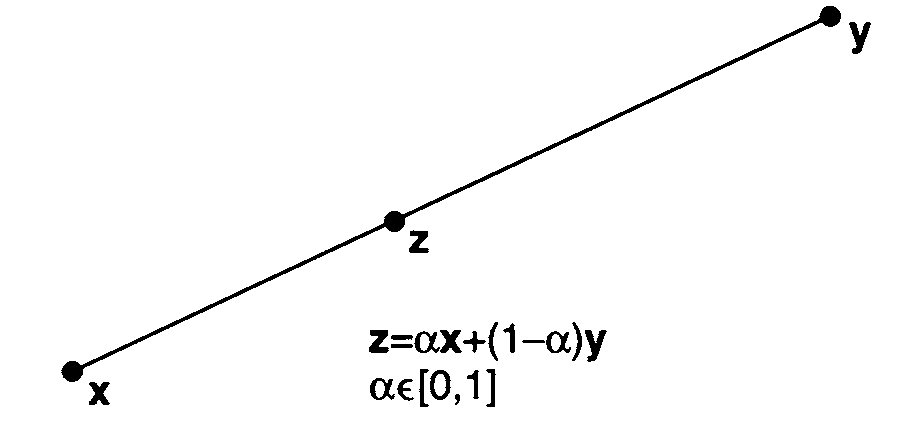
$\mathbb{R}^{n}$서 두점 $x$와 $y$사이의 $\boldsymbol{line \ segment}$는 점 $x$와 $y$를 접합하는 직선 상의 점 집합입니다.
$z$가 $x$와 $y$ 사이의 $\boldsymbol{line \ segment}$에 있는 경우는 아래와 같이 정의할 수 있습니다.
$$z-y=\alpha (x-y)$$
$\alpha$는 $[0,1]$ 사이의 실수. 위의 방정식은 $z=\alpha x+(1-\alpha)y$로 다시 쓸 수 있으므로, 따라서 $x$와 $y$ 사이의 $\boldsymbol{line \ segment}$는 아래와 같이 나타낼 수 있습니다.
$$\left \{\alpha x + (1 - \alpha) y : \alpha \in [0,1] \right \}$$
'Optimization > Concept From Geometry' 카테고리의 다른 글
| Hyperplane (0) | 2021.07.01 |
|---|---|
| 초평면 (Hyperplane) (0) | 2021.07.01 |
Comments
