| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- neural network
- 딥러닝
- machine learning
- 리스트
- reinforcement learning
- Deep Learning
- optimization
- list
- 논문
- Jacobian Matrix
- convex optimization
- 사이킷런
- unity
- 모두를 위한 RL
- 데이터 분석
- 판다스
- Series
- paper
- Linear algebra
- pandas
- Python Programming
- Laplacian
- statistics
- 강화학습
- ML-Agent
- rl
- Hessian Matrix
- 유니티
- David Silver
- 김성훈 교수님
RL Researcher
Lecture 6: Value Function Approximation 본문
Lecture 6: Value Function Approximation
Lass_os 2021. 2. 4. 16:59
RL은 다음과 같이 큰 문제들을 풀 수 있습니다
- Backgammon Game : $10^{20}$개의 State
- Computer Go : $10^{170}"$개의 State
- Helicopter : 연속적인 공간 내에서 움직이기 때문에 값이 무한적입니다.

지난 2개의 강의에서 배웠던 Model-Free 메소드인 MC, TD에서 Prediction과 Control 문제를 어떻게 확장할 수 있을까요?

위의 질문에 답을 할 수 있는 Value Function Approximation을 통해서 Scale up이 가능합니다.
- 우리는 전 강의들 까지는 lookup table 방식으로 value function을 표현해 왔습니다.
- $V(s)$는 State $s$의 개수만큼 빈칸이 존재했습니다.
- $Q(s,a)$는 모든 state-action의 pair개수 만큼 빈칸이 존재했습니다.
- 큰 MDP에서의 문제는
- 이러한 큰 State나 Action들 같은 경우는 memory에 담을 수 없습니다.
- 다 담을 수 있다고 하더라고 각 State에 대해 배우는 것이 너무 느립니다.
- 큰 MDP의 문제에서의 해결책은:
- function approximation을 통해 value function을 추정합니다.
$$\hat{v}(s,w) \approx v_{\pi}(s)$$
$$or \ \hat{q}(s,a,w) \approx q_{\pi}(s,a)$$
- 우리가 보지 못했던 state에 대해서도 올바른 value에 맞도록 output이 나옵니다.
- MC와 TD 학습방법을 이용해서 Parameter Value $w$값을 업데이트합니다.

- $v$는 위의 그림과 같이 state를 blackbox에 집어넣으면 output값을 도출하는 것입니다.
- $v$와 다르게 $q$는 $s,a$값을 넣어 해당하는 $q$값을 도출할 수도 있고(Action-in), $s$만 집어넣어 $s$에서 가능한 모든 Action $q$값을 뽑을 수도 있습니다.(Action-out)

Function Approximator에는 다양한 것들이 쓰일 수 있습니다.
- feature들에 대한 선형조합
- 인공신경망
- 의사결정나무
- KNN
- ...

우리는 이 중에서 미분가능한 Function approximator를 사용할것입니다.(미분을 통해 Gradient를 구하여 w를 업데이트 할 수 있기 때문)
- feature들의 선형조합
- 인공 신경망
이 방법은 모분포가 계속 바뀌고 서로 독립적이지도 않습니다.(Correlation)

- $J(w)$라는 함수는 w라는 n demension vector parameter값을 넣으면 값이나온다고 가정합시다.
- 우리는 이 $J(w)$라는 함수를 최소화 하는 $w$값을 찾고 싶습니다.
$$\triangledown_{w}J(w) = \begin{pmatrix}
\frac{\partial J(w)}{\partial w_{1}}\\
:\\
\frac{\partial J(w)}{\partial w_{n}}
\end{pmatrix}$$
- $J(w)$라는 함수의 지역 최저값을 찾는 것
- $w$ vector값은 Gradient의 방향을 알려줍니다.'
$$\triangle w = -\frac{1}{2}\alpha \triangledown_{w}J(w)$$
- $\alpha$는 step-size parameter입니다.

- 목표는 추정함수 값인 $\hat{v}(s,w)$와 참함수 값인 $v_{\pi}(s)$ 사이의 MSE값을 최소화하는 n demension vector $w$값을 찾는 것입니다.
$$J(s) = E_{\pi}[(v_{\pi}(S) - \hat{v}(S,w))^{2}]$$
- 경사하강법으로 지역 최저값을 찾습니다.
$$\triangle w = -\frac{1}{2}\triangledown_{w} J(w) = \alpha E_{\pi}[(v_{\pi} (S) - \hat{v}(S,w))\triangledown_{w} \hat{v}(S,w)]$$
- 샘플 경사를 이용한 것이 확률적 경사 하강법입니다.
$$\triangle w = \alpha(v_{\pi}(S) - \hat{v}(S,w)) \triangledown_{w} \hat{v}(S,w)$$
- 예상되는 값은 완전히 경사를 업데이트한 것과 같습니다.

선형 조합의 Feature들의 선형조합을 Value Function으로 사용하는 것을 설명하고 있ㅅ브니다.
$$x(S) = \begin{pmatrix}
x_{1}(S)\\
:\\
x_{n}(S)
\end{pmatrix}$$

- Feature들의 선형조합의 가치함수에 대해서 표현해보겠습니다.
$$\hat{v}(S,w) = x(S)^{T}w = \sum_{j = 1}^{n}x_{j}(S)w_{j}$$
- 목적함수는 parameter $w$의 2차형식입니다.
$$J(w) = E_{\pi}[(v_{\pi}(S) - x(s)^{T}w)^{2}]$$
- 확률적 경사하강법은 전역 죄척으로 수렴합니다.
$$\triangledown_{w} \hat{v}(S,w) = x(S)$$
$$\triangle w = \alpha(v_{\pi}(S) - \hat{v}(S,w)) \times(S)$$
- 업데이트 수식 = step-size x prediction error x feature value

- Table lookup은 선형값 함수 근사값의 특별한 경우입니다.
- Table lookup feature를 사용한 경우
$$x^{table}(S) = \begin{pmatrix}
1(S = s_{1})\\
:\\
1(S = s_{n}
\end{pmatrix}$$
- parameter $w$는 개별적인 State에대한 값들을 줍니다.
$$\hat{v}(S,w)\begin{pmatrix}
1(S = s_{1})\\
:\\
1(S = s_{n})
\end{pmatrix} \cdot\begin{pmatrix}
w_{1}\\
:\\
w_{n}
\end{pmatrix}$$

- 우리는 이때까지 supervisor가 True Value function인 $v_{\pi}(s)$값을 알려줬다고 가정하고 수식을 진행했었습니다.
- 하지만 RL은 supervisor가 존재하지 않으며, 오직 보상만 존재합니다.
- 이제는 우리가 배웠던 $v_{\pi}(s)$값에 MC와 TD를 이용할 것입니다.
- MC에서는 target은 반환값 $G_{t}$입니다.
$$\triangle w = \alpha(G_{t} - \hat{v}(S_{t}, w))\triangledown_{w} \hat{v}(S_{t},w)$$
- TD(0)에서는, target은 TD target $R_{t+1} + \gamma \hat{v}(S_{t+1},w)$ 값입니다.
$$\triangle w = \alpha(R_{t+1} + \gamma \hat{v}(S_{t+1}, w) = \hat{v}(S_{t}, w))\triangledown_{w} \hat{v}(S_{t},w)$$
- TD($\lambda$)에서는 $\lambda$-return $G^{\lambda}_{t}$ 값입니다.
$$\triangle w = \alpha(G^{\lambda}_{t} - \hat{v}(S_{t}, w))\triangledown_w \hat{v}(S_{t},w)$$

- Return $G_{t}$는 편향되지 않고, true value $v_{\pi}(S_{t})$의 nosiy sample입니다.
- training data에 supervised learning을 적용하면 다음과 같이 됩니다.
$$<S_{1},G_{1}>,<S_{2},G_{2}>, ..., <S_{T}, G_{T}>$$
- MC 평가방법은 지역 최적에 수렴합니다.
- 비선형 함수 근사를 사용하여도 잘 수렴합니다.

- TD-target을 위의 $G_{t}$값에 넣어 업데이트가 가능하며 true value $v_{\pi}(S_{t})$의 편향된 값입니다.
- 선형 TD(0)는 전역 최적값에 가깝게 수렴합니다.

- TD($\lambda$)에 대해서도 위와 같이 값을 집어넣을 수 있습니다.

- Forward view와 Backward view의 선형 TD($\lambda$)값은 같습니다.

- 이때까지는 Prediction문제, 즉 Value-fucntion을 찾는 것에 대한 문제를 풀고 있었습니다. 이제부터는 Policy를 찾는 문제인 Control문제에 대한 것을 알아보겠습니다.

- q를 구하는 문제는 어렵지 않습니다. 앞서 배웠던 v자리에 q만 써주면 되는 것입니다.(A도 포함)
- MSE값을 최소화하는 것입니다.
- 지역 최적값을 찾기 위해서 확률적 경사하강법을 사용합니다.

- 위와 같이 똑같은 Feature 생성이 가능하며
- 이 Feature들의 선형조합을 행동가치함수로 표현이 가능합니다.

- q대신에 return, TD(0), Forward TD($\lambda$), Backward TD($\lambda$)를 집어넣을 수 있습니다.

- 앞서 배웠던 q자리에 다양한 것들을 집어넣어 policy evaluation을 수행하고, $\epsilon$-greedy를 이용하여 policy improvement를 수행합니다. 우리는 이 알고리즘을 Linear Sarsa라고 부릅니다.


- 위의 그림은 Control문제를 풀 때 Bootstrap이 필요하다라는 예시입니다

- 항상 TD(0)가 수렴하지 않는다라는 것을 보여주기 위한 예시를 설명하고 있습니다.

- 어떠한 경우에는 값이 점점 발산하는 것을 볼 수도 있습니다.

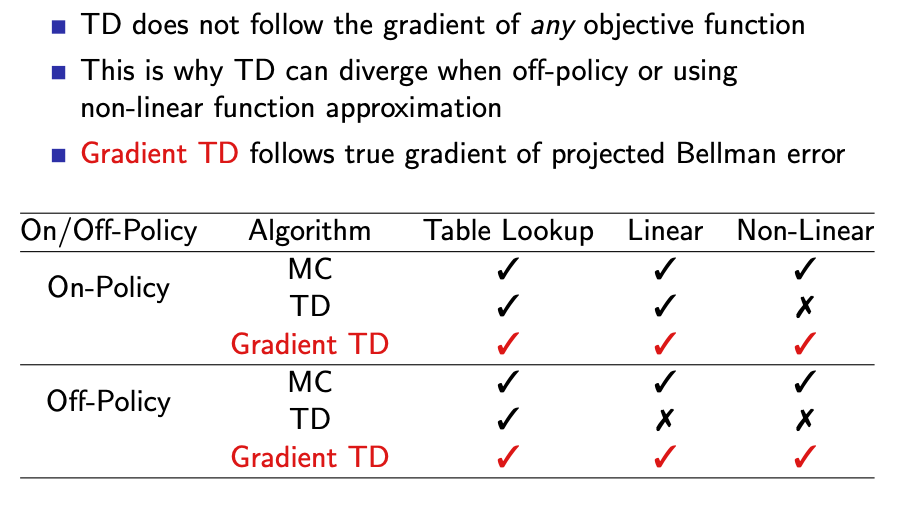
- Gradient TD는 non-linear일 때나 off-Policy일 때도 수렴성이 좋다고 발표하였습니다.

- Control 문제도 다음과 같은 수렴성을 보입니다.

- 한번 업데이트 하고 쓰인 것은 사용되지 않기 때문에 샘플 자체가 효과적이지 못합니다.
- Agent가 쌓은 경험을 training data처럼 반복해서 사용하면서 학습을 수행하는 것입니다.


- State와 value를 Sampling을 통해서 Stochastic Gradient Descnet를 적용합니다.
- Experience Replay 방법은 off-policy를 수행할 때 많이 사용하는 방법입니다.


- 다음은 Atari game에 대한 예시를 들면서 수식을 설명하고 있습니다.(Experience Replay를 설명하기 위함인 것 같음)
- DQN에서는 Experience replay와 fixed Q-target이 사용됩니다.
- Replay Memory에 $(s_{t}, a_{t}, r_{t+1}, s_{t+1})$와 같은 transition을 저장합니다.
- mini-batch를 통해서 Replay Memory에서 Random하게 뽑습니다.
- 학습은 Least Square를 줄이는 것입니다.(TD-target과 Q의 제곱의 차이를 줄이는 것)
- fixed Q-target은 예전 파라미터들을 고정시켜놓고 현재의 parameter를 돌리고, 계속 업데이트하는 방식입니다.

















'Reinfrocement Learning > David-Silver Lecture' 카테고리의 다른 글
| Lecture 7: Policy Gradient (0) | 2021.02.17 |
|---|---|
| Lecture 5: Model-Free Control (0) | 2021.02.03 |
| Lecture 4: Model-Free Prediction (0) | 2021.02.03 |
| Lecture 3: Planning by Dynamic Programming (0) | 2021.02.02 |
| Lecture 02 : Markov Decision Processes (0) | 2021.02.02 |




